
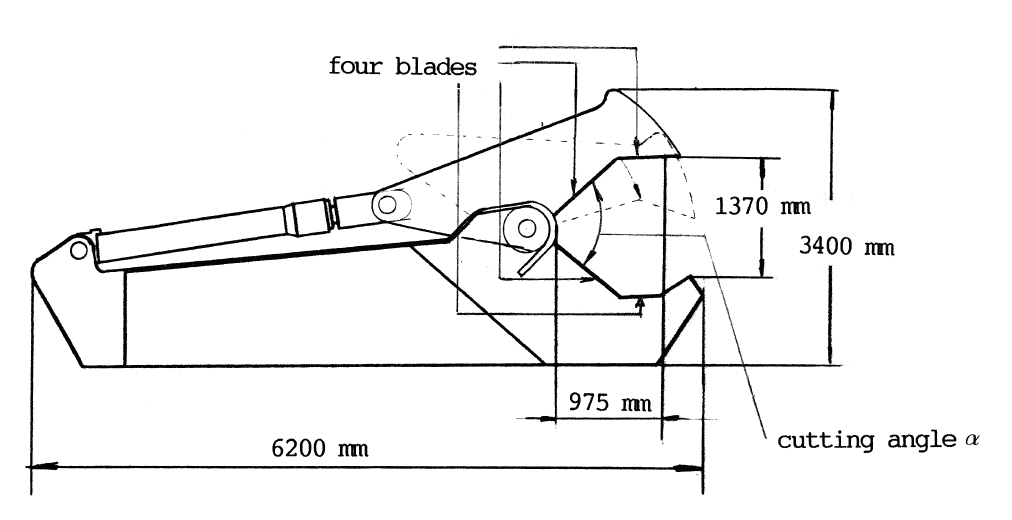
| {1}: | Fdef = C * Mp * (D/t)½ |
| C | = | factor related to jaw shape of the shear and extend of deformation | |
| Mp | = | plastic moment per unity of length | |
| = | σy * ( t2 / 4 ) | ||
| t | = | wall thickness | |
| σy | = | yield stress | |
| D | = | tube diameter |
| Fcut > Fdef |
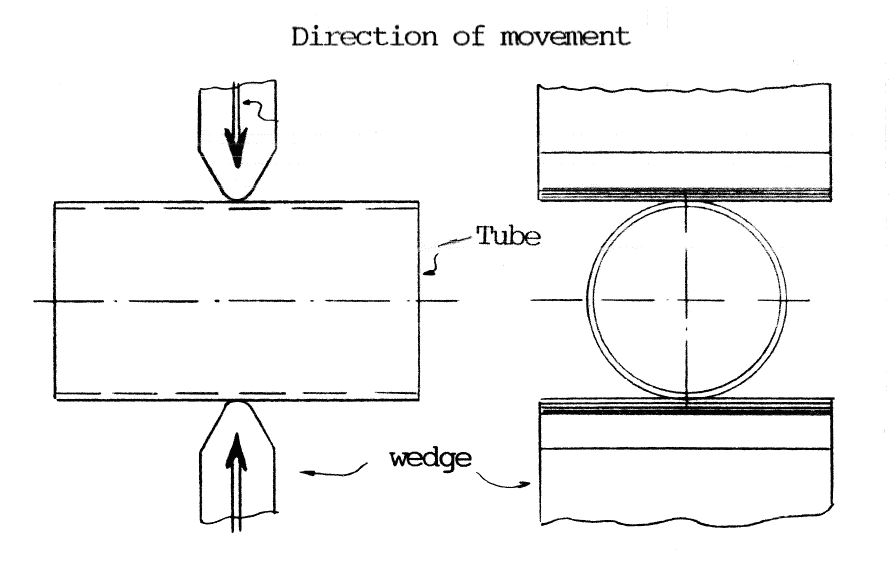

| {2}: | Fmax = 55 * Mp * (D/t)½ |
| Fmax > 55 * Mp * (D/t)½ |
| {3}: | Fshear = A * 0.8 * σt |
| Fshear | load required for shearing shear | ||
| A | = | area of material between the blades of the shear | |
| σt | = | tensile strength of material to be cut |
| {4}: | Acrosss-sectional < 0.8 * Fcut / ( 0.8 * σt ) |

